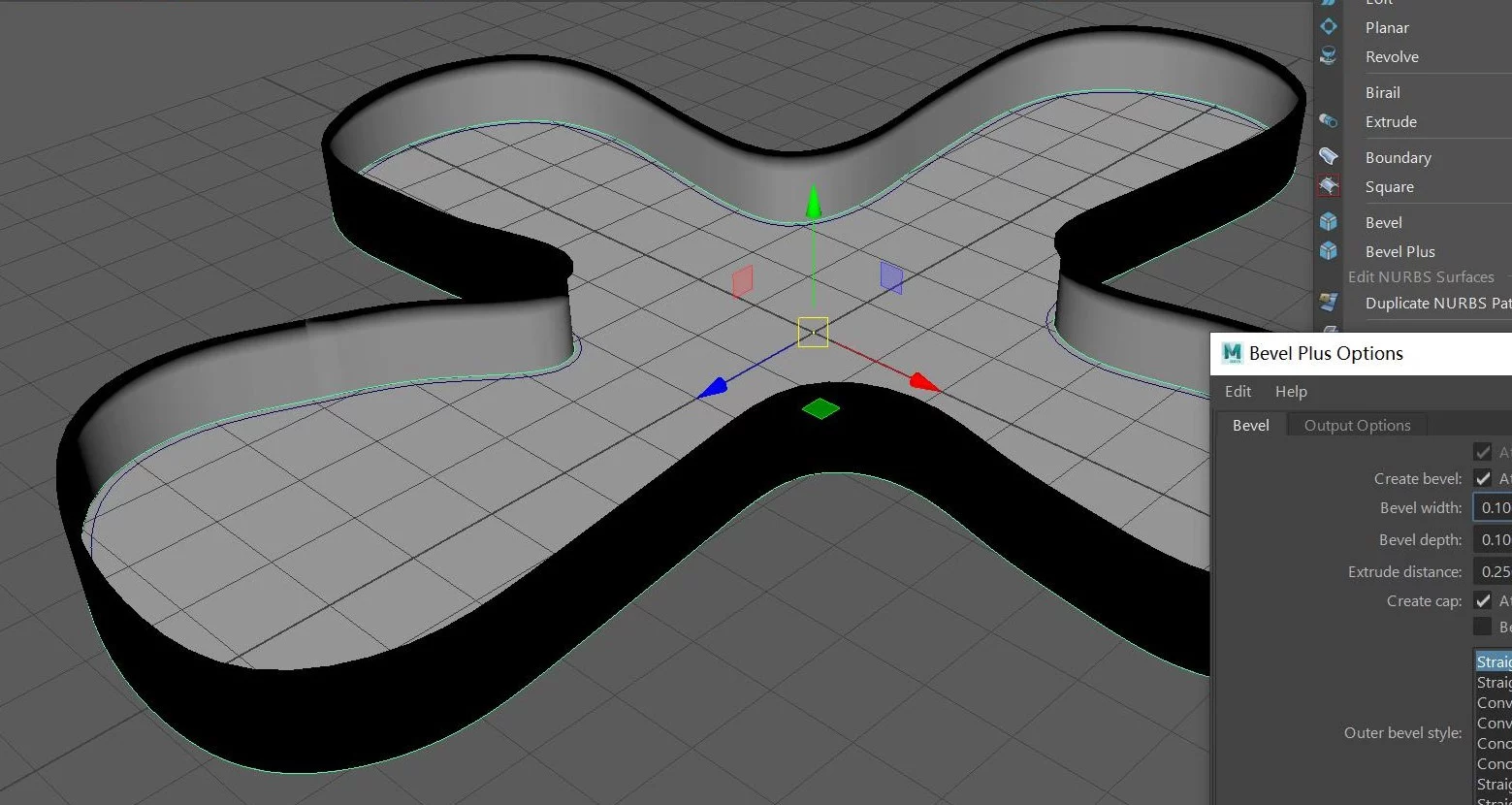
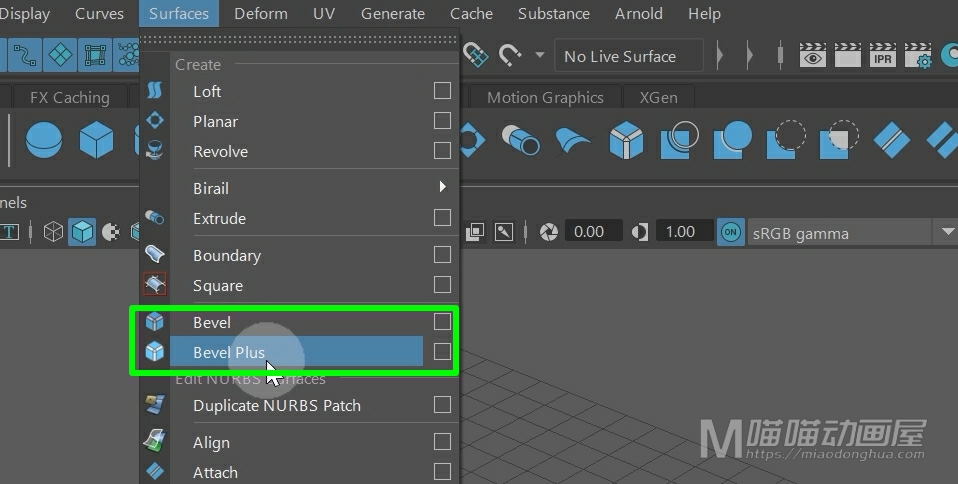
今天我们来看一下Maya曲面菜单下的这个倒角命令(Bevel)和这个倒角+命令(Bevel Plus)。那么它们两者的作用都是通过对曲线倒角来达到生成曲面的目的。
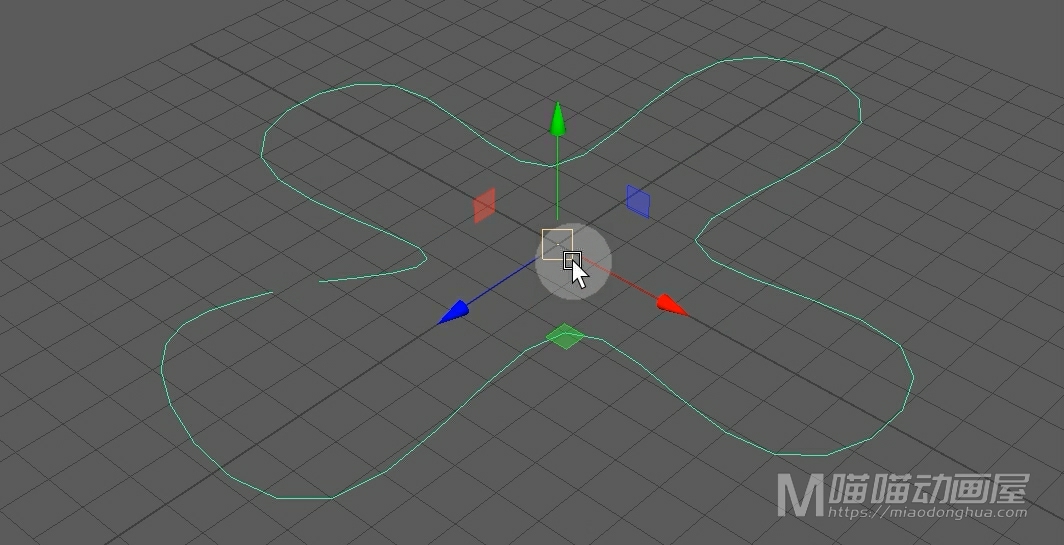
例如我们使用EP曲线工具在场景中绘制出一个曲线轮廓。那么平时我们在制作的时候,一定要保证我们的曲线是闭合状态。那么很显然,我们的这条曲线是没有闭合的。
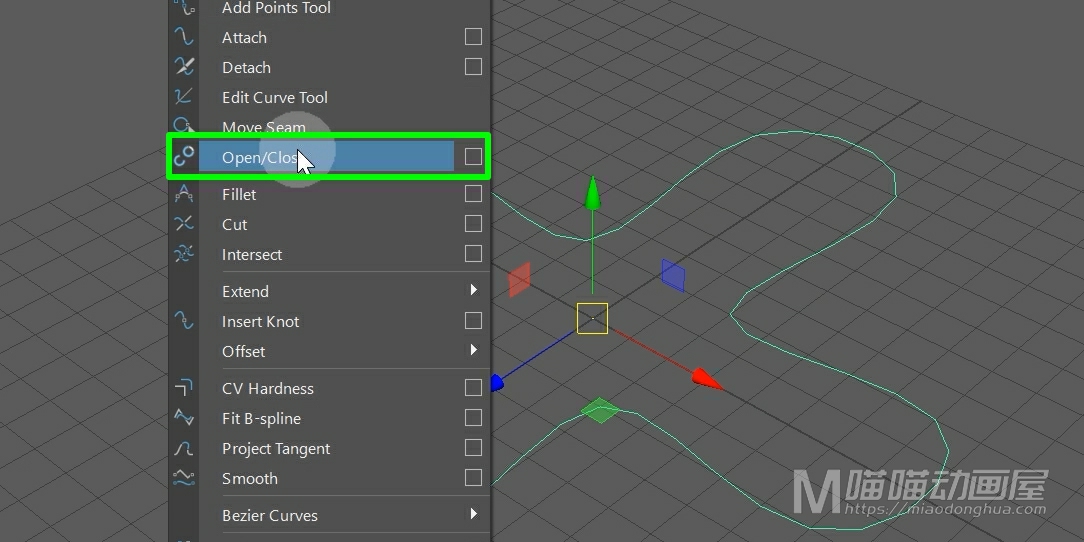
我们可以在曲线菜单下,选择执行开放/闭合曲线。
这样我们的曲线就变成了闭合曲线。

那么为了在构建曲面的时候让模型表面过度更加的均匀和平滑。我们可以在曲线菜单下,选择重建选项。
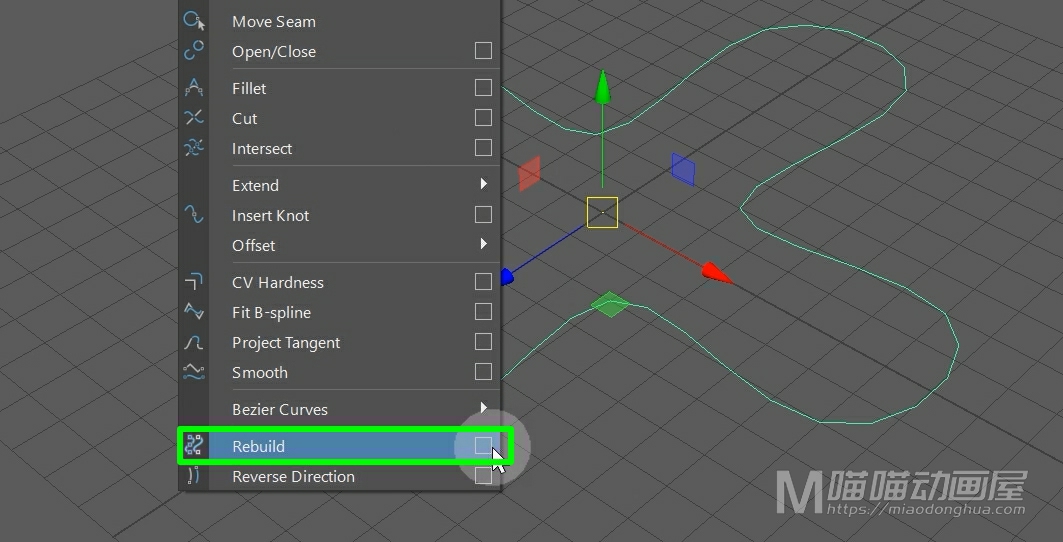
这里我们可以把它的分段数设置为50,然后点击重建。
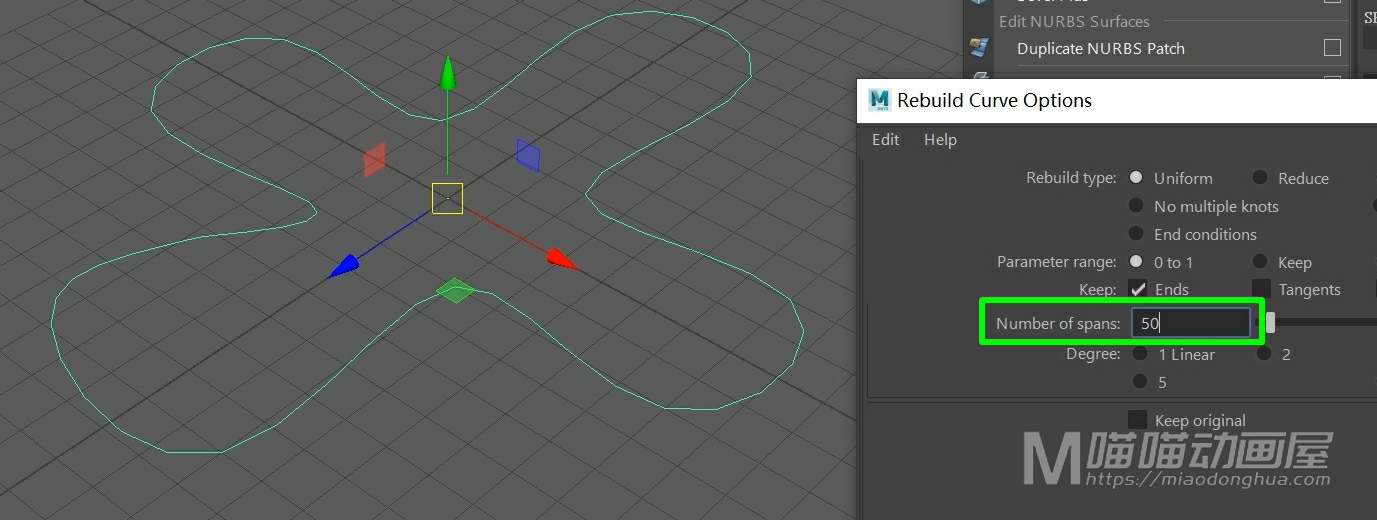
然后我们选择执行倒角命令。
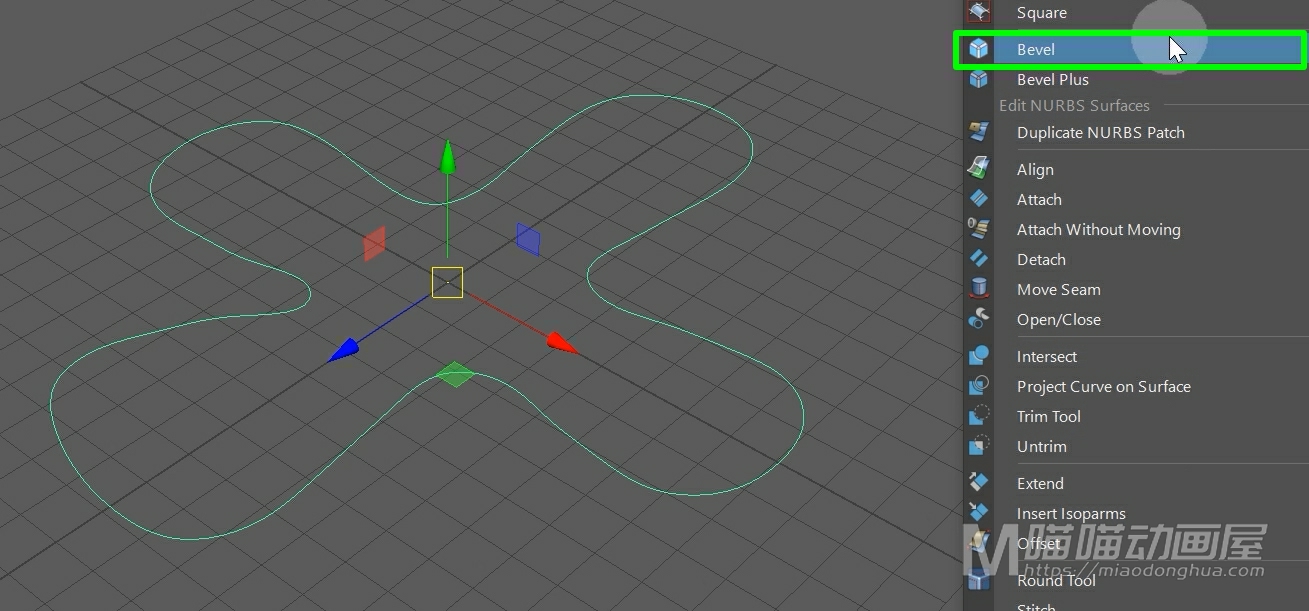
这样我们的这个曲面就构建出来了。

我们可以看到:这个曲面实际上是一个整体。如果我们要把倒角面和挤出面分开,我们可以打开倒角选项设置,在这里取消勾选这个附加曲面就可以了。
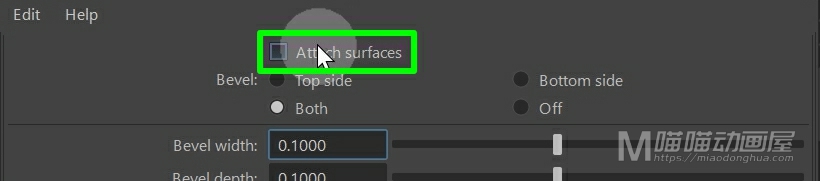
我们把这个曲面模型删除,我们重新选择曲线,然后点击应用。这样,我们的这个倒角曲面和挤出曲面就是分离开的。
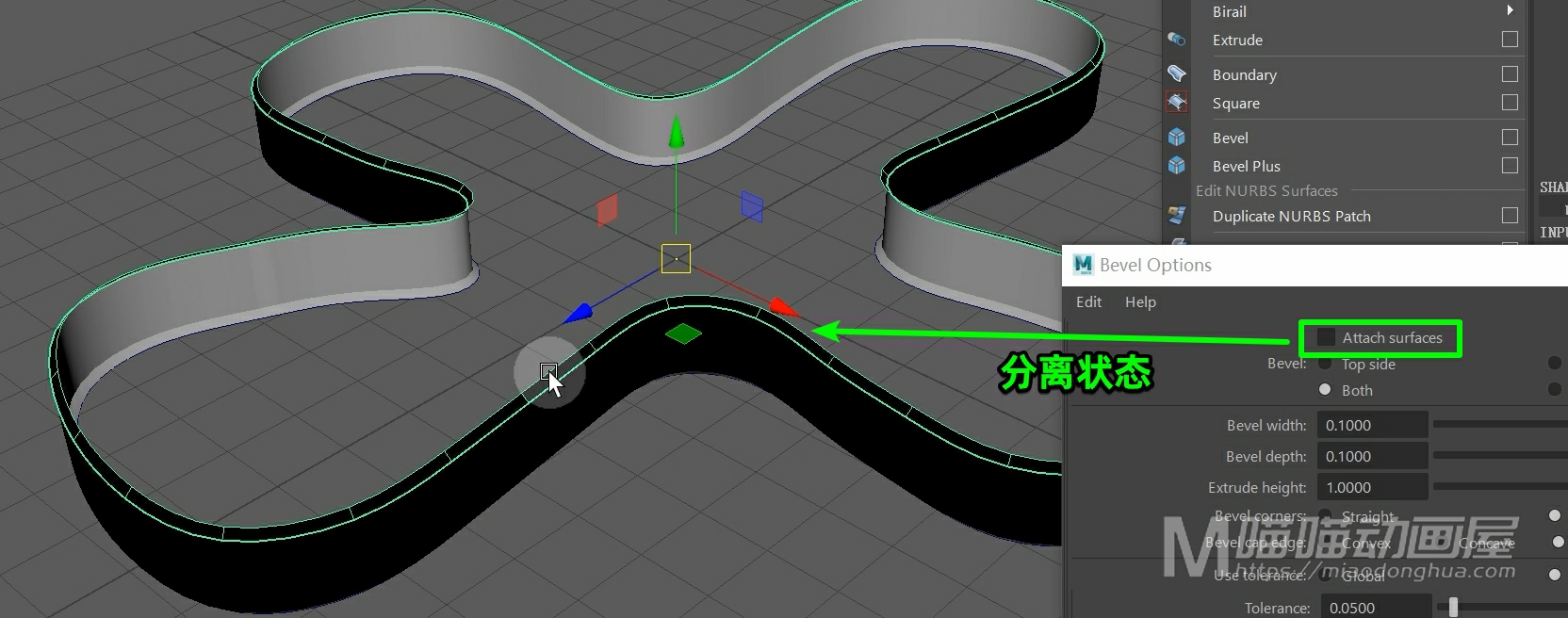
接着我们可以在通道盒中的输入节点中,对形状做进一步的修改。那么这个宽度,就是指倒角的宽度。
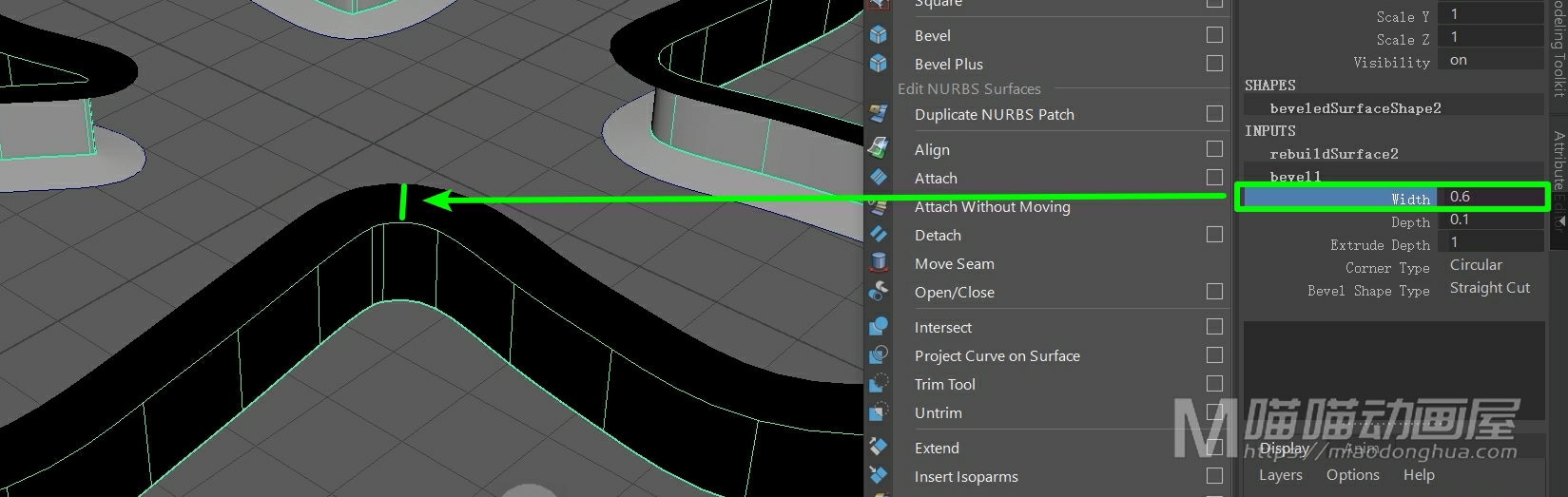
这个深度,就是指我们成面倒角部分的高度。
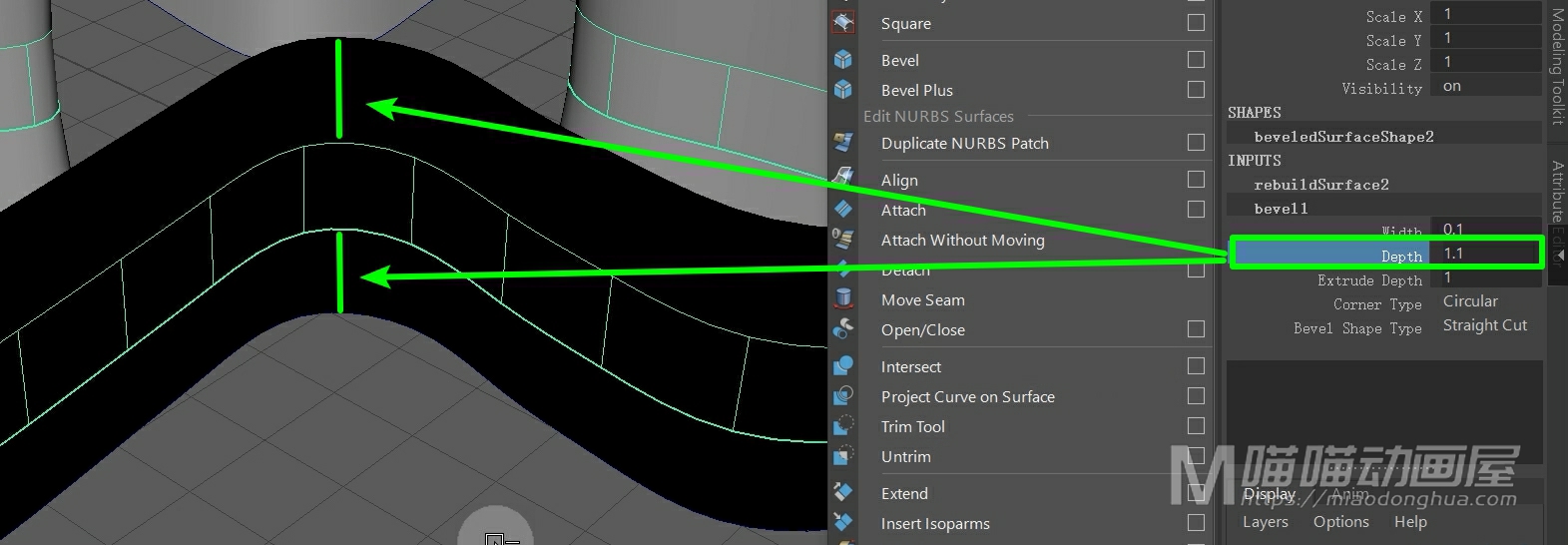
而这个挤出深度,它指的是倒角以外,中间部分的高度。至于下方的角点类型和倒角形状类型,一般保持默认就可以了。
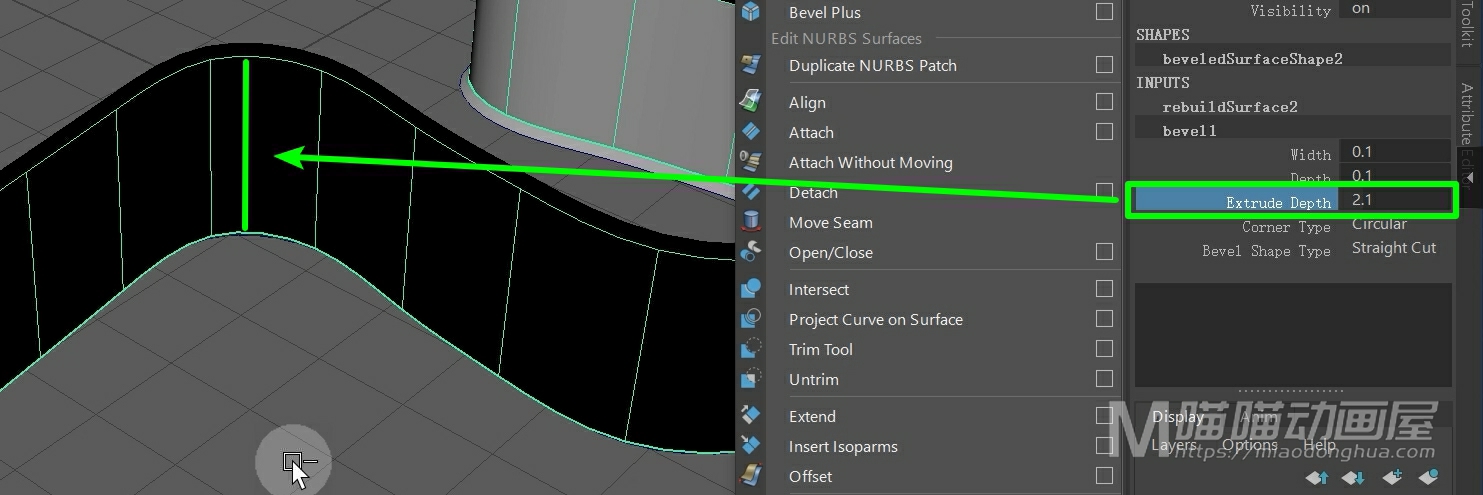
另外假设我们只想倒角一侧,我们可以打开倒角选项设置。在这里就有一个倒角选项,默认是从两边创建倒角。
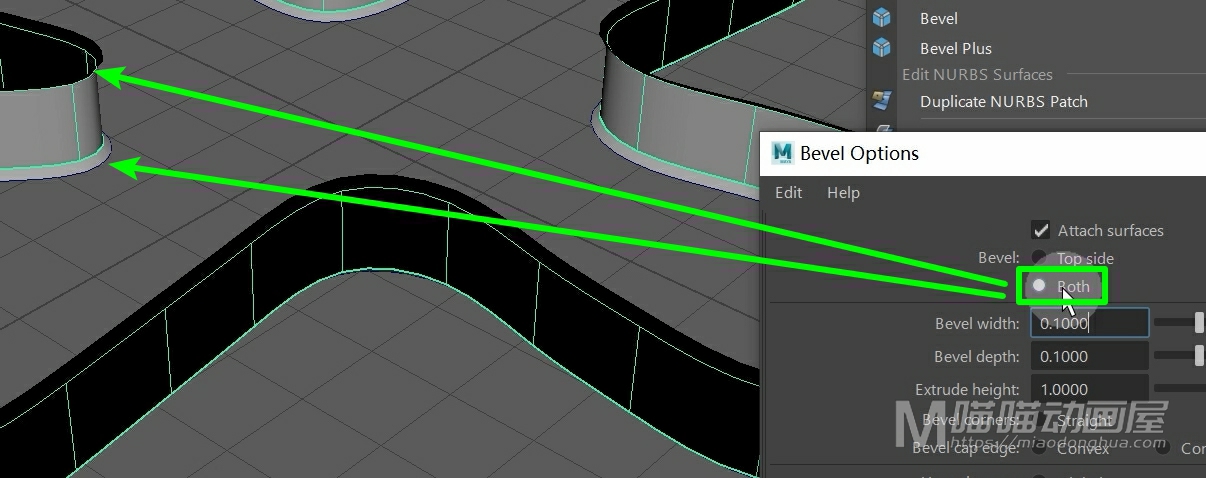
我们可以根据自己的需要选择从顶边、底边或者是关闭倒角都是可以的。
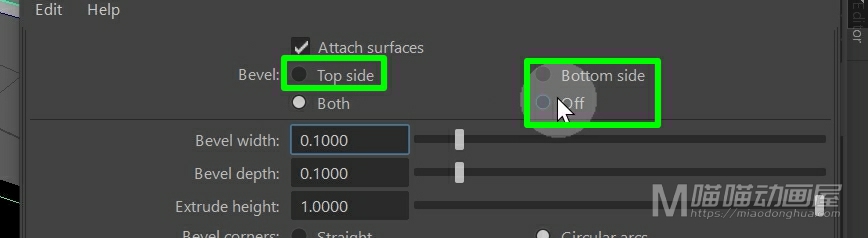
这里我们选择一个从底边创建,我们先把这些曲面删除,我们重新选择曲线,然后点击应用。这样,另外一侧就不会创建倒角曲面,这个很简单,这里就不多说了。
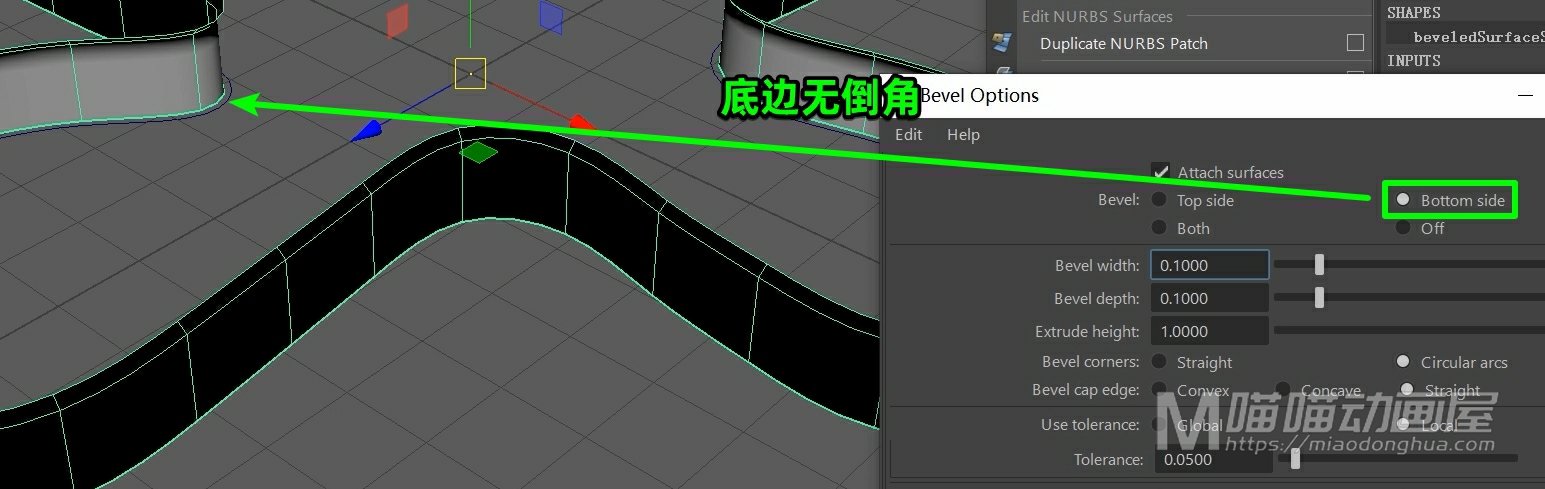
那么这个曲面是制作出来了,我们还必须知道:怎么给这个曲面构建出一个封口?那么因为这个曲面上的等位线是在同一平面上的,所以我们可以进入等位线模式,选择底部边缘上的等位线,然后执行平面成面命令。
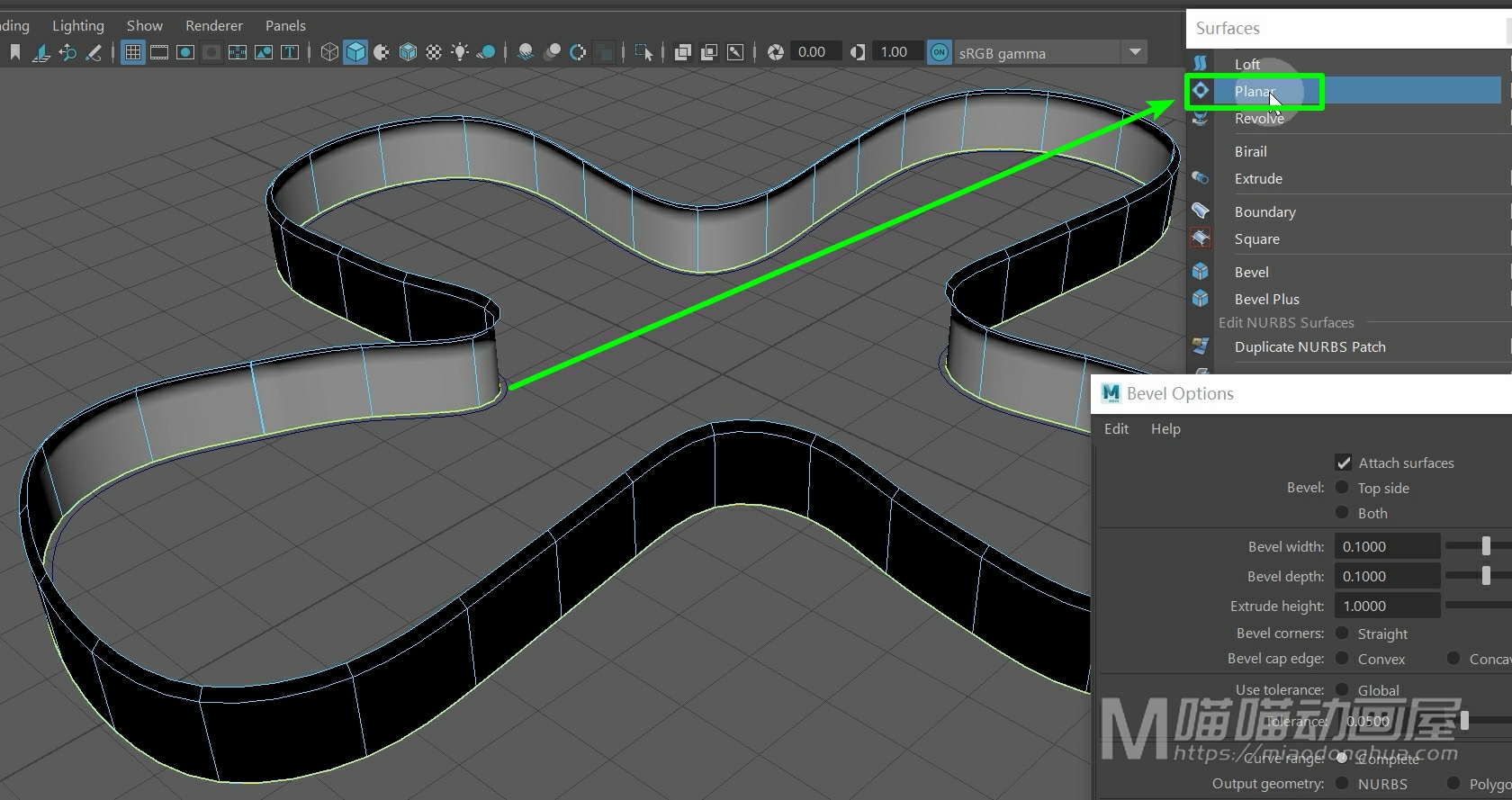
这样,我们的这个底部封口平面就制作好了,非常方便。
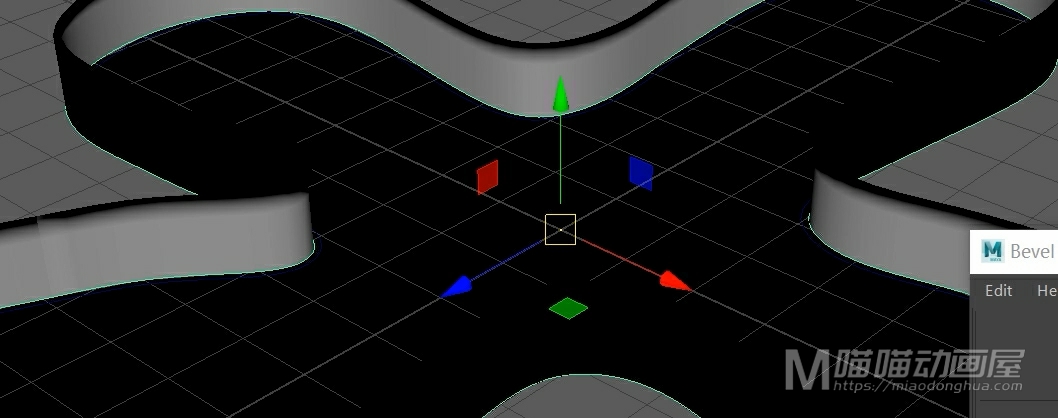
另外,我们可以点击反转方向,让封口曲面和其他曲面统一。
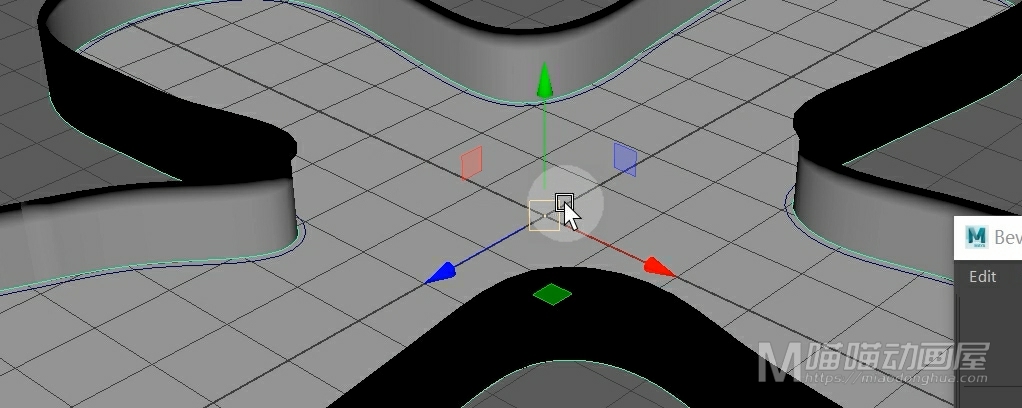
然后,我们再来看下这个倒角+命令,我们打开它的选项设置,那么这个命令说白了就是倒角命令的升级版。那么比较大的区别就是:这个倒角+命令默认的输出类型是多边形。
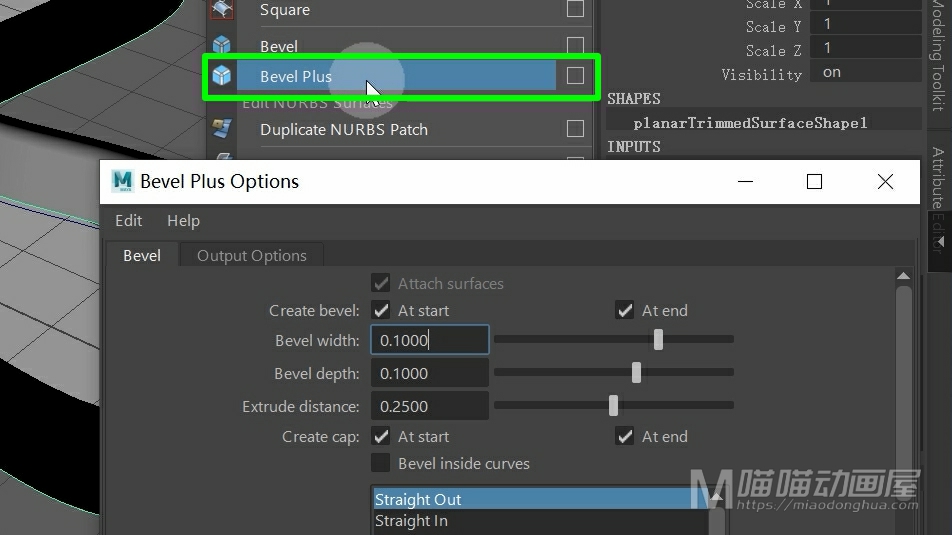
虽然我们上面的这个倒角命令也可以输出多边形。但是我们的这个倒角+生成的多边形要更加的美观,更符合我们日常的使用需求。并且这里的倒角选项,直接简化为开始或者是在结束的部分倒角,非常的简洁,易于使用。
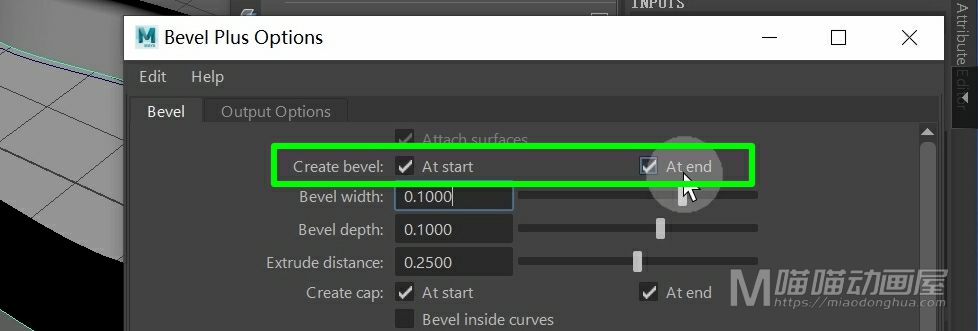
还有这个封口,我们可以选择在开始或者是结束部分封口,相比我们的这个手动创建封口要方便的多。
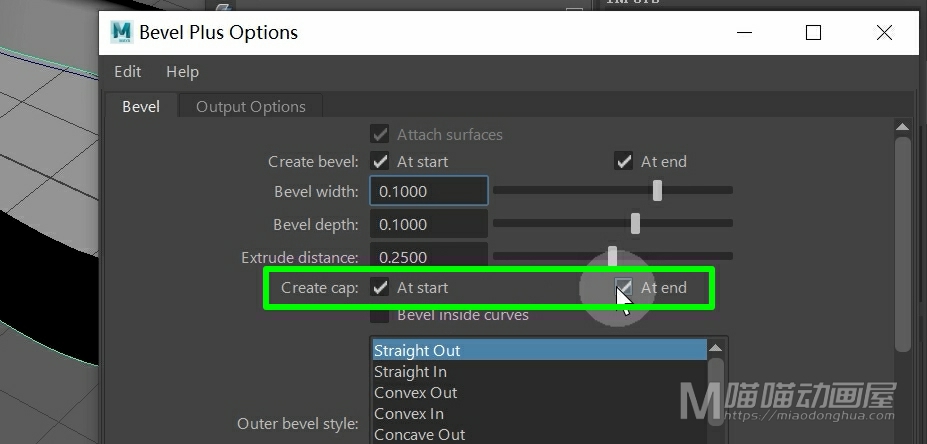
另外,这里提供了非常多的倒角类型:直出,直入等等,功能非常的强大。
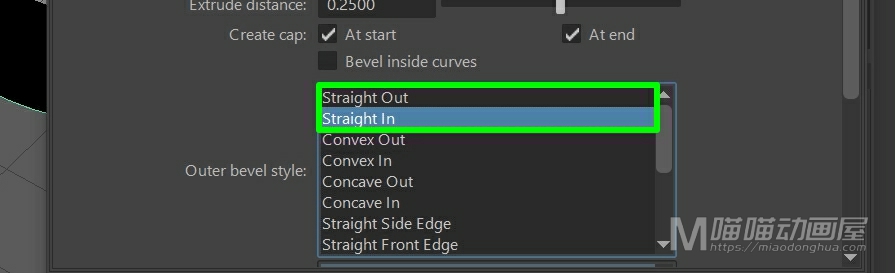
我们先把这些个曲面删除,我们先来看下默认状态下的倒角成面效果,我们选择曲线,然后点击应用。我们可以看到,我们生成的这个多边形,它的布线是非常美观的。
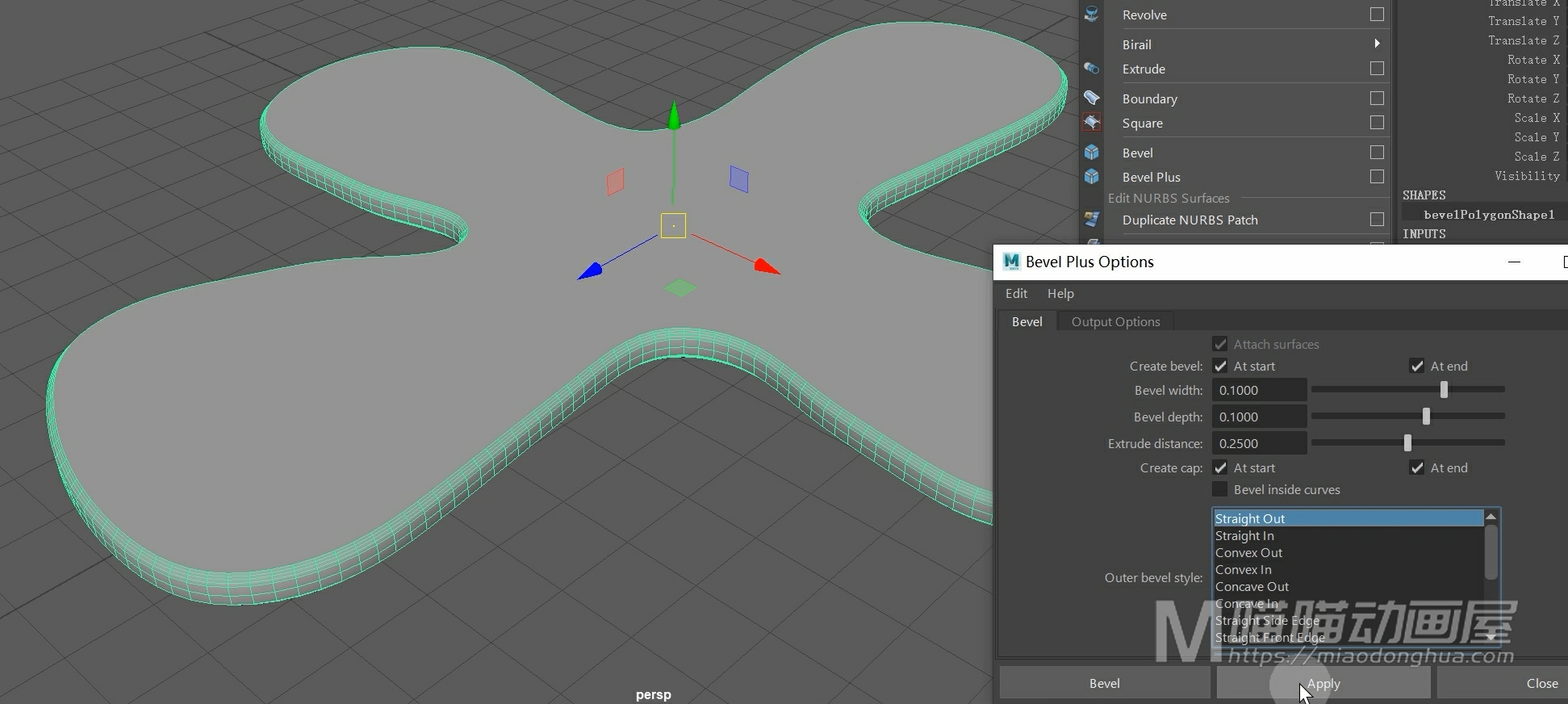
假设我们要把模型中间的部分向内延伸。

我们可以把它的这个输出倒角类型设置为:直入。
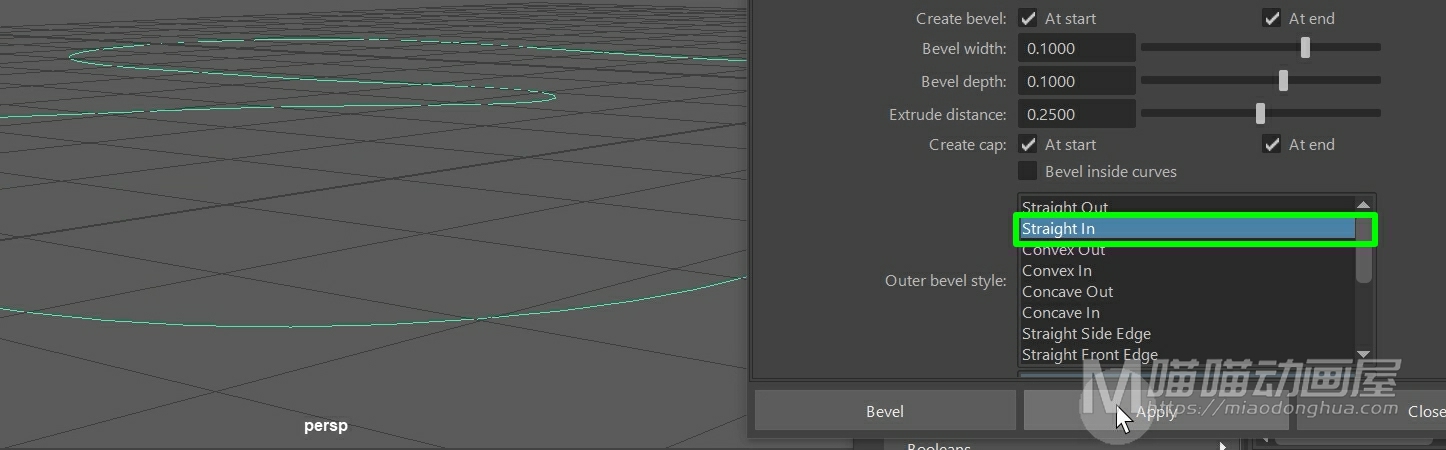
我们把这个模型删除,我们重新选择曲线,然后点击应用。这样,这个模型中间挤出部分就会变为向内延伸。
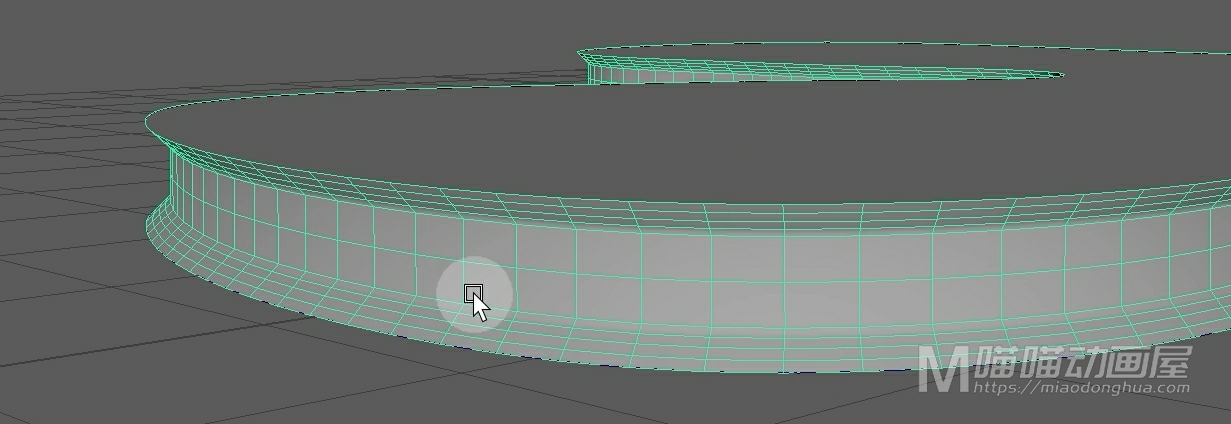
至于其它的样式,我们可以自己下去慢慢的研究。
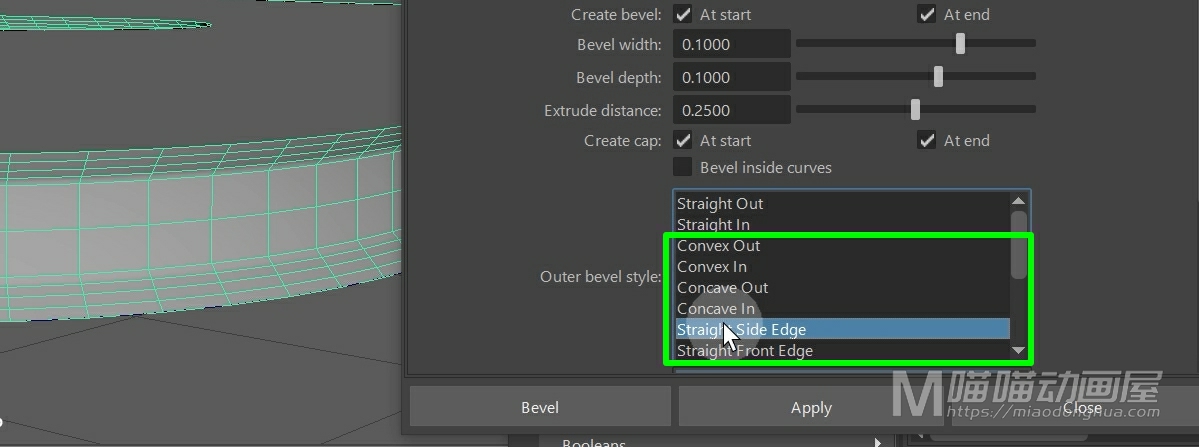
好了,关于倒角成面主要就是这些内容。